The Art of Birth Photography: Tips and Techniques for Stunning Entries
By Aaron
Published February 19, 2024
 The Art of Birth Photography: Tips and Techniques for Stunning Entries
The Art of Birth Photography: Tips and Techniques for Stunning Entries
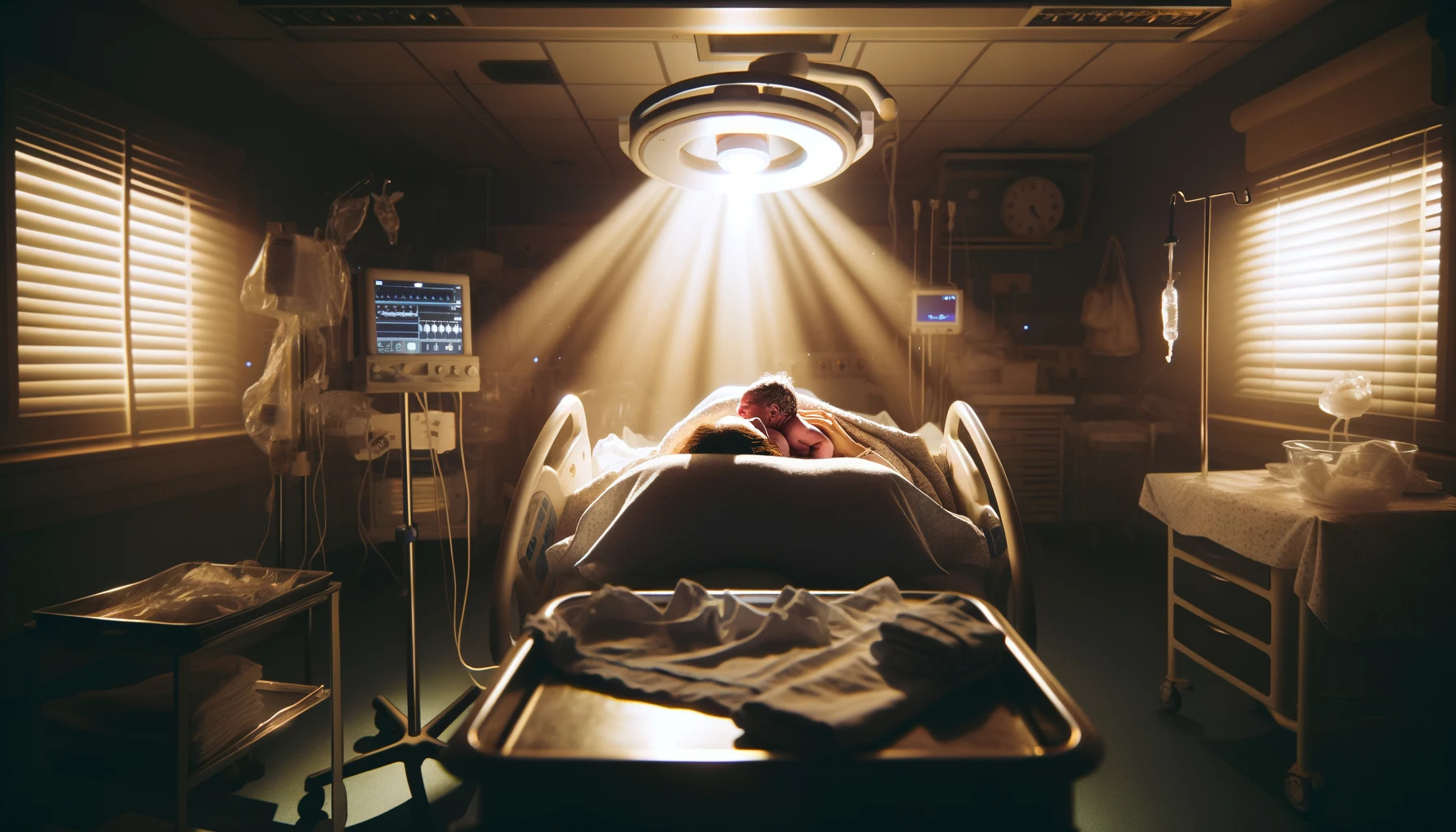
Birth photography captures the raw, unfiltered essence of life's beginning, often immortalizing these moments into cherished baby wallpapers for many families. It's an art form that requires not just technical prowess, but a deep sensitivity to the moments and the people involved. Aspiring birth photographers have the unique opportunity to document these once-in-a-lifetime moments, turning them into timeless memories. Here, we explore essential tips and techniques to help you create stunning entries for any birth photography showcase.
Understanding the Essence of Birth Photography
Birth photography goes beyond mere snapshots; it's about storytelling, capturing the intensity, love, pain, and joy of childbirth. It's important to approach this genre with respect, empathy, and a readiness to capture the fleeting moments that define the start of a new life.
1. Technical Preparedness
- Low Light Mastery: Birth rooms are often dimly lit to create a comfortable environment for the mother. Mastering low light photography is crucial. Invest in a good quality camera that performs well in such conditions and familiarize yourself with its settings to avoid using flash, which can be intrusive.
- Fast Lens: A fast lens with a wide aperture (f/2.8 or wider) will allow you to capture sharp images in low light conditions without sacrificing the quality.
- Silent Shutter: Utilize your camera’s silent shutter mode to minimize distractions, ensuring a respectful presence.
2. Emotional Intelligence
- Building Rapport: Establish a strong, trusting relationship with the family. Being a calming presence in the room allows you to capture genuine emotions while being respectful of the space.
- Anticipation: Learn to anticipate moments before they happen. This means understanding the stages of labor and being ready to capture key expressions and events.
3. Composition and Framing
- Diverse Perspectives: Don’t just focus on the baby; capture the environment, the expressions of family members, and the mother’s journey. These elements contribute to the storytelling aspect of your photography.
- Use of Baby Backgrounds: Incorporate the baby background creatively to add depth and context to your images. This can be done by using the natural environment of the birth room or by post-processing.
4. Post-Processing
- Upscale Image: Utilize tools to upscale images without losing quality, ensuring that even the softest details are preserved and highlighted.
- Background Remover: In some cases, removing the background can focus more on the subject. Tools that offer free SVG or free PNG options can be particularly useful for creating cleaner, more focused images.
- Free Image Hosting: Consider using free image hosting services to share your work with clients securely and efficiently, allowing them to access their photos anytime, anywhere.
The Art of Captivity
1. Sensitivity to the Environment
Being acutely aware of your surroundings and the people in it is paramount. Birth photography is not just about capturing a good shot but doing so in a way that is non-invasive and supportive of the birthing process.
2. Narrative Through Images
Each photograph should tell a part of the story. Whether it’s the pain of a contraction or the first time a mother holds her child, these images together narrate the profound journey of childbirth.
3. The Decisive Moment
Henri Cartier-Bresson's concept of the "decisive moment" is incredibly relevant in birth photography. It’s about capturing the emotion, the action, and the environment in a fraction of a second that tells a complete story.
Ethics and Privacy
1. Consent is Key
Always have clear, written consent from all parties involved before photographing. This not only includes the birthing parent but also any family members and healthcare providers present.
2. Respect Privacy
Be mindful of what you capture and share. Some moments are incredibly private, and it's essential to respect the family's wishes regarding what images are kept private and which can be shared publicly.
Final Thoughts
Birth photography is a powerful, emotive field that requires technical skill, emotional intelligence, and a deep respect for the birthing process and all involved. By mastering the technical aspects, such as understanding how to work in low light conditions and utilizing tools for post-processing like upscale image software, background remover tools, and free image hosting services, you can elevate your work. Remember, it's not just about the images you capture but the story you tell and the memories you preserve for families at one of the most pivotal moments of their lives.
By following these tips and techniques, you're well on your way to creating stunning, meaningful birth photography that captures the beauty and intensity of childbirth. Remember, each birth is unique, and each photo is a testament to the miraculous journey of life.